Calculus

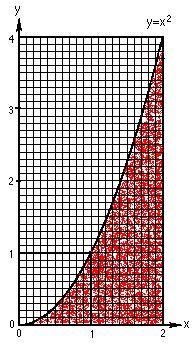
Calculus makes it possible to find the area under a curve, such as the areas shown in figures 1 and 2. This can't be done with ordinary math.. With calculus the equation for the curve, such as  "Y = X squared"  in figure, can be manipulated so that you can compute the exact area.

 Calculus also enables us to find the "slope" of a curve at a given point, as shown in figure 3. This is also not possible with ordinary math.

This may not seem like a big thrill, for those of you who aren't wild about math, to be able to do things ordinary math can't, but we ask you to bear with us and learn to do these basic manipulations, integration and differentiation, and look at what they mean. If you do you have a basic grasp of these procedures you can look at a level of math that has a kind of magic to it.  You can peer into higher math, a strange and, in a way beautiful world that goes beyond systems of reckoning.

We would like readers to note that calculus sat in front of mathematicians' faces for about 20 centuries. The early Greek  mathematicians knew the formulas for the circumference and area of a circle, and they knew the formulas for the surface area and the volume of a sphere, but no one noticed that the change in formula from circumference to area is the same as the change in formula from surface area to volume, as we show below.  These two changes are similar because they both go from the formula for outer envelope to the formula for what is contained: the circumference is like a fence around a field, which is the area, the thing contained. The surface area is like a balloon around the volume of air it contains. It is natural for mathematicians to look for consistencies in the math when comparing similar geometric transitions, but in the case of calculus no one picked up on it from around 300 BC to after 1700 AD.

Below are figures illustrating the concept of the area under a curve and the slope of a curve.

figure 1 Area under curve	figure 2   Area under curve.	figure 3   Slope of a curve at a point on the curve.

Below, in math 1 and math 2, are two examples of "integration", the manipulation which enables us to find the area under a curve.  In math 1 the formula for a the graph in figure 1, is on top, the integral is below it. The manipulation consists of adding 1 to the "exponent" of X, which is 2, giving 3, and then inverting that number getting 1/3, and multiplying. In math 2, likewise, a formula (usually called a "function" of X) is on top, the integration of that function is below it. We add 1 to the exponent, 5, getting 6, then invert the six and multiply. In math 3 we give the general formula for integration, with n substituting for any exponent of X.

math 1     is the integral of	math 2   integration of "X to the fifth"	math 3      integration of  Y = X to any exponent n

To compute the area under the curve in figure 1 for X = 2, Y = 4, we plug 2 for X into  , which is the integral of  , and get 8/3.  That calculation is shown below. We also show the calculation for X = 3 which gives an area of 9. If the graph were in inches, the area would be 9 square inches, under the curve from X = 0 to X = 3.

	The graph in question, , is not shown for the value X = 3, Y = 9 in figure 1 above.
math 4  We plug values for X into the integral of , which is

Below is integral calculus as observed in the the change from the formula for the circumference of a circle to the formula for the area of  a circle. It is  the same change, the same manipulation, which  we performed above, except r is the "variable" instead of  X. As with going from the line of the graph to the area under that line, in the case of the circle we go from the line of the circle, the circumference, to the area contained by that line. Since r has no exponent we say it has an exponent of 1, which is the way exponents work. To perform the integration we therefore add 1 to 1, giving 2, then invert the 2, giving 1/2, and multiply, yielding the formula for the area, "pi r squared."

The circumference is integrated to give the area, red boxes, stated two ways.

We restate the same integration below. C = circumference.

Integration also takes us from the formula for the surface area of a sphere to the formula for the volume of a sphere, as shown below. The surface area is the area of the outside surface of an object,  measured in square units, like square inches if you were measuring a the surface area of a ball, or square miles if you were measuring the surface area of a planet. The principle of this integration is  the same as going from circumference to area: the formula for the thing contained, the area or the volume, is found by integrating the formula for the figure that contains. The circumference contains the area, like a fence around a field. The surface area contains the volume, like a balloon contains a volume of air.

The surface area S integrates to the volume V. This is stated two ways in the red boxes.

We restate the same integration below. S = surface area of a sphere.

page in progress.  Derivatives to be presented.